Merci à Robert Ehrlich et Emmanuel Lazard, qui m’ont signalé les erreurs qui figuraient dans une première version de cet article. Emmanuel m’a fourni la plupart des schémas électroniques de cet article, ainsi que les textes qui leur correspondent, je lui suis doublement redevable de ce fait. Les erreurs qui pourraient subsister seraient de mon fait uniquement.
Transistor
L’unité centrale de l’ordinateur, et notamment l’unité arithmétique et logique, est constituée de circuits logiques. Les circuits logiques réalisent matériellement les opérations de la logique, et à partir de là les opérations arithmétiques élémentaires. Il suffit, pour réaliser les circuits logiques nécessaires à toutes les opérations, d’un dispositif unique, dit semi-conducteur, qui en fonction d’un courant de commande laisse passer ou bloque un courant entre une source et un drain. C’est ce que nous allons montrer.
Le premier semi-conducteur fut la triode, inventée en 1906 par Lee De Forest et utilisée dans la construction de l’ENIAC et des premiers ordinateurs comme dans celle des anciens postes de radio « à lampes » et de luxueux amplificateurs, mais nous passerons tout de suite à son équivalent moderne, le transistor, dont l’invention aux Bell Laboratories en 1947 vaudra le prix Nobel 1956 à John Bardeen, Walter Houser Brattain et William Shockley.
Je n’entreprendrai pas l’explication des phénomènes physiques en jeu dans le transistor, que toute bonne encyclopédie en ligne ou sur papier révélera au lecteur, et je me bornerai au modèle donné par figure ci-dessous, qui correspond à un transistor bipolaire. Les circuits actuels utilisent plutôt des transistors à effet de champ, qui autorisent des densités plus élevées, mais avec des circuits plus complexes, et le but de cette page n’est pas un cours d’électronique. Pour une présentation analogue avec des transistors à effet de champ, on pourra par exemple se reporter au site d’Olivier Carton. Signalons aussi la réédition récente de l’ouvrage de Paolo Zanella, Yves Ligier et Emmanuel Lazard, Architecture et technologie des ordinateurs, aux Éditions Dunod, et la conférence de François Anceau dans le cadre d’un séminaire au Conservatoire des Arts et Métiers.
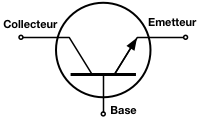
Figure 1 : Modèle du transistor bipolaire NPN : quand la base est mise à une tension positive, le courant passe du collecteur à l’émetteur ; quand la base est mise à une tension négative ou nulle, le courant ne passe pas.
Algèbre de Boole
Munis du dispositif très simple qu’est le semi-conducteur (qu’il soit réalisé par une triode ou des relais peu importe), les ingénieurs des premiers circuits logiques (George Stibitz des Bell Labs en 1937, l’Allemand Konrad Zuse en 1938, et à plus grande échelle Eckert et Mauchly pour l’ENIAC) s’attaquèrent aux opérations de l’algèbre de Boole. Le mathématicien britannique George Boole (1815 - 1864) avait imaginé de formaliser la logique d’Aristote au moyen d’une algèbre d’événements qui depuis porte son nom.
Soit un ensemble d’événements A, B, C, .... À chaque événement correspond une proposition : l’événement considéré a eu lieu. Nous considérons un ensemble d’événements qui ont entre eux un certain rapport de contenu, en ceci qu’ils sont liés au résultat d’une seule et même épreuve. À chaque épreuve est attaché un certain ensemble de résultats possibles ; de chacun des événements on doit pouvoir affirmer, pour chaque résultat de l’épreuve, s’il a eu lieu ou non [1].
Si deux événements A et B, pour chaque résultat de l’épreuve, sont toujours ou tous deux réalisés, ou tous deux non-réalisés, nous dirons qu’ils sont identiques, ce qui s’écrit A=B.
La non-réalisation d’un événement A est aussi un événement, qui s’écrira $\bar{A}$.
Rényi prend pour épreuve l’exemple du tir sur une cible et propose de partager la cible en quatre quadrants par un diamètre vertical et un diamètre horizontal. L’événement A sera réalisé si le coup frappe la moitié supérieure de la cible, l’événement B si le coup frappe la moitié droite de la cible.
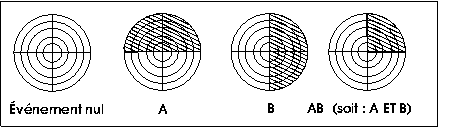
Figure 2 : Exemples d’événements
Si A et B ont eu lieu tous les deux, il s’agit d’un nouvel événement, C, qui est justement « A et B ont eu lieu tout les deux », qui a lieu si le coup frappe le quadrant supérieur droit de la cible. C’est le produit de deux événements, que nous noterons A ET B ou A.B ou simplement selon l’élégante notation de Rényi :
C = AB
De même, on peut se demander si au moins un des deux événements A et B a eu lieu. La proposition « au moins un des deux événements A et B a eu lieu » est vraie si le coup ne frappe pas le quadrant inférieur gauche de la cible. Cet événement qui se produit quand au moins un des deux événements A et B a lieu est appelé la somme de A et B et s’écrit A OU B ou $A \cup{} B$ ou simplement : C = A + B.
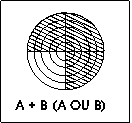
Figure 3 : Ou logique
Nous n’irons guère plus loin en algèbre de Boole. Le lecteur pourra vérifier les propriétés algébriques du produit et de la somme, qui sont « bonnes ». Nous pouvons donner les tables de vérité de ces opérations :
| a | b | ab | a+b |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| a | $\bar{a}$ |
| 0 | 1 |
| 1 | 0 |
Réalisation des opérations booléennes
Cette section doit beaucoup au livre de Patrick de Miribel Principe des ordinateurs [2]. Emmanuel Lazard a réalisé les schémas et les textes explicatifs qui leur correspondent.
Par convention, le vrai sera représenté par la valeur 1 et le faux par la valeur 0. À la valeur 1 correspondra un courant positif et à la valeur 0 un courant nul.
Les circuits ci-dessous comportent des résistances, symbolisées par des fils en zigzag, qui comme leur nom l’indique font obstacle au passage du courant. Si le courant trouve un chemin plus facile, comme par exemple un transistor à l’état passant, il ne franchira pas la résistance (plus exactement, le courant qui franchira la résistance sera faible et inférieur au seuil qui le rendrait efficace). Mais s’il n’y a pas d’autre chemin, par exemple parce que le transistor est à l’état bloqué, le courant franchira la résistance.
Circuit NON
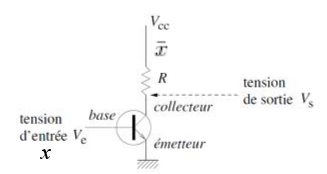
Figure 4 : Circuit NON
Si x = 0, la base du transistor est à un potentiel nul, le transistor est bloqué ; via la résistance, le courant positif va arriver en $\bar{x}$ qui vaudra donc 1, ce qui est bien le contraire de 0.
Si x = 1, le courant positif atteint la base du transistor qui devient passant. De ce fait, le point $\bar{x}$ est directement relié à la masse, donc à une tension nulle et vaudra 0, ce qui est le résultat voulu.
Circuit OU
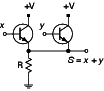
Figure 5 : Circuit OU
Nous avons deux transistors en parallèle : pour que le courant positif parvienne à la sortie notée x + y et lui confère ainsi la valeur 1, ou le vrai, il suffit que l’un des deux transistors soit passant. Pour cela il suffit que l’une des deux entrées, x ou y, soit positive : en effet un courant positif en x par exemple l’emportera sur la mise à la masse générée par R. C’est bien le résultat attendu.
Circuit ET
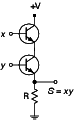
Figure 6 : Circuit ET
Nous avons deux transistors en série : pour que le courant positif atteigne la sortie notée xy il faut que les deux transistors soient passants, et donc que les deux entrées x et y soient positives, ce qui est bien le résultat voulu, conforme à la sémantique du ET.
Complétude de cette réalisation
Il existe d’autres opérations booléennes, mais il est aisé de démontrer qu’elles peuvent toutes se ramener à une composition des trois opérations que nous venons de voir. Il existe d’autres façons de réaliser une algèbre de Boole complète, notamment avec la seule opération NON ET (NAND), souvent utilisée par les circuits contemporains : plus touffue pour le lecteur humain, elle donne des résultats strictement équivalents à ceux que nous venons de décrire. Ce circuit est décrit par la figure 7.
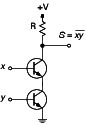
Figure 7 : Circuit NON ET (NAND)
Comme les circuits NON OU (NOR) et OU EXCLUSIF (XOR) sont aussi utiles, notamment pour réaliser la mémoire, les voici dans les figures 8 et 9.
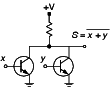
Figure 8 : Circuit NON OU (NOR)

Figure 9 : Circuit OU EXCLUSIF (XOR)
Construction de l’arithmétique
Munis d’une réalisation électronique de l’algèbre de Boole, nous allons montrer que nous pouvons réaliser les opérations de l’arithmétique binaire. En fait, nous allons montrer comment réaliser un opérateur électronique capable d’additionner deux chiffres binaires et de donner un chiffre de somme et un chiffre de retenue. En combinant plusieurs exemplaires de ce circuit de base il est possible de construire un additionneur à plusieurs chiffres. L’addition donne la multiplication et la soustraction, qui donne la division : autant dire que l’on a tout. Le lecteur peu assuré de sa connaissance de l’arithmétique binaire pourra se reporter au texte sur la numération binaire.
Voici la table de vérité du semi-additionneur binaire. Soient s le chiffre de somme et r la retenue. Leibniz avait déjà remarqué la conséquence simplificatrice de l’usage de la numération binaire : la retenue et le chiffre de somme n’ont que deux valeurs possibles, 0 ou 1 (cf. le texte de Leibniz).
| x | y | s | r |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
De cette table nous pouvons inférer, par comparaison avec les tables des opérations logiques ci-dessus :
$r = xy$
$s = (x + y) \cdot \overline{xy}$
s = (x OU y) ET NON (x ET y)
Opérations que nous pouvons réaliser par le circuit de la figure 10.
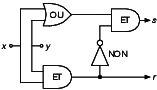
Figure 10 : Semi-additionneur binaire
Construction de la mémoire
Mémoire statique
Jusque dans les années 1970 la mémoire était réalisée à partir d’éléments statiques, le plus souvent des tores de ferrite dont l’orientation du champ magnétique représentait conventionnellement la valeur d’un bit.
Aujourd’hui la mémoire est réalisée avec des circuits logiques, le plus souvent des portes NON OU (NOR). Voici la table de vérité de NON OU, qui comme son nom l’indique donne des résultats opposés à ceux du OU :
| x | y | x NOR y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Une position de mémoire élémentaire, qui représente un bit, est obtenue en combinant deux circuits NON OU de telle sorte que la sortie de l’un alimente l’entrée de l’autre, et réciproquement. Un tel dispositif est appelé une bascule (latch en anglais), représentée par la figure 11.
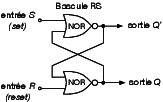
Figure 11 : Élément de mémoire : bascule statique
Selon la table d’opération ci-dessus, la sortie d’une porte NON OU vaut 1 si toutes ses entrées sont à 0. Selon les tensions appliquées à ses entrées R (comme reset, remettre le bit à 0) et S (comme set, allumer le bit à 1), les sorties Q et Q’ ont les valeurs indiquées dans la table ci-dessous :
| S | R | Q | Q’ | {{}} |
| 1 | 0 | 1 | 0 | Set (allumer) |
| 0 | 0 | 1 | 0 | Le bit vaut 1 |
| 0 | 1 | 0 | 1 | Reset (éteindre) |
| 0 | 0 | 0 | 1 | Le bit vaut 0 |
| 1 | 1 | 0 | 0 | État interdit |
Le dernier état correspondrait à une situation où l’on demanderait au circuit de positionner le bit simultanément à 0 et à 1, ce qu’il semble raisonnable d’exclure. Q’ a toujours la valeur complémentaire de celle de Q, soit NON Q, noté $\bar{Q}$.
On observera que la combinaison de deux objets élémentaires, ici deux portes NON OU, crée un objet qui excède de beaucoup ses composants en richesse conceptuelle : une position de mémoire est un objet beaucoup plus complexe qu’une porte logique, l’algèbre de Boole ne peut pas en rendre compte.
Mémoire dynamique
La mémoire décrite ci-dessus est statique, elle nécessite pour conserver sa valeur une tension constante.
Les mémoires les plus courantes, parce que les plus denses et les moins chères, sont les mémoires dynamiques, réalisées en technologie à effet de champ. Une position de mémoire est créée en utilisant la charge emmagasinée par la capacité grille-drain d’un transistor MOS comme élément de mémoire. L’isolation d’un tel circuit n’est jamais parfaite, donc il se décharge progressivement, et il faut le recharger avant que la charge ne tombe sous le seuil en dessous duquel elle n’est plus significative. Cette opération s’appelle le rafraîchissement.
